Емпірична функція розподілу
Нехай маємо статистичний розподіл деякої ознаки Х (кількість балів, оцінка).
Позначимо через п загальну кількість спостережень (об’єм вибірки), kх – кількість спостережень при яких спостережувана ознака Х х. Тоді відносна частота події Х х дорівнює
.Якщо х змінюється, то може змінюватись і відносна частота, тобто
є функцією відх. Оскільки її знаходять дослідним шляхом, то вона має назву емпіричної.Означення. Емпіричною функцією розподілу (або функцією розподілу вибірки) називають функцію F*(x), яка визначає для кожного значення х відносну частоту події Х х
F*(x)=
.Інтегральна функція F(x) генеральної сукупності у математичній статистиці називається теоретичною функцією розподілу. Так як F(x) – ймовірність того, що F(x)=Р(Х х), а F*(x)=
події Х х прямує також до ймовірності цієї події, то функції F(x) і F*(x) мало відрізняються одна від одної.Властивості емпіричної функції розподілу
0≤ F*(x) ≤1.
F*(x) – зростаюча.
F*(x)=
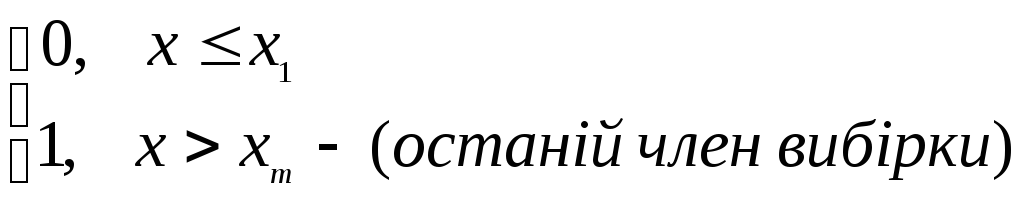.34.Полігон та гістограма
З метою створення візуального відображення статистичної інформації користуються різними графіками. Найпоширеніші види графічного відображення статистичної інформації — це полігони і гістограми. Графічне зображення варіаційних рядів за допомогою полігона чи гістограми допомагає отримати наочне уявлення про закономірності про можливі зміни спостережуваних значень.
Полігон, як правило, використовують для відображення дискретного варіаційного ряду.
Полігоном частот називають ламану з вершинами у точках (zі, ni), i = 1, 2, ..., k. Тут zi — значення і-ї варіанти, а пi — відповідна цій варіанті частота.
Для побудови полігона частот на осі абсцис відкладають варіанти z„ а на осі ординат — відповідні частоти. Точки (zі, ni) сполучають відрізками прямих і отримують полігон частот.
Зобразимо полігон частот варіаційного ряду, заданого таблицею 1.
Таблиця 1
| xi | 1,5 | 3,5 | 6 | 9 |
| | 0,1 | 0,2 | 0,4 | 0,3 |
По суті, полігон частот — це графічне зображення інтервального ряду (мал. 1).
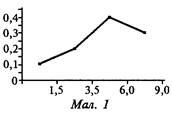
Полігоном відносних частот називають ламану, відрізки якої сполучають точки (z1, ), (z2, ), …, (zk, ) — тобто це статистичне зображення статистичного розподілу.
Зазначимо, що можлива побудова полігона частот не тільки для дискретного варіаційного ряду, а й для інтервального статистичного ряду. В ситуації з інтервальним статистичним рядом при побудові полігонів як абсциси відповідних кінців відрізків обирають точки .
Гістограми використовують для зображення винятково інтервальних варіаційних рядів. Для її побудови в прямокутній системі координат на осі абсцис відкладають відрізки, що є частковими інтервалами спостережень. На цих відрізках, як на основах, будують прямокутники з висотами, що дорівнюють частотам — абсолютним або відносним. Тобто розглядають два типи гістограм. Варто знати формальне означення гістограми.
Гістограмою абсолютних частот називають ступінчасту фігуру, яка побудована з прямокутників, основою яких є інтервали групування, довжини h, а висоти дорівнюють
Площа гістограми абсолютних частот дорівнює п.Гістограмою відносних частот (або просто гістограмою) називають ступінчасту фігуру, яка складається з прямокутників, основами яких є часткові інтервали групування довжини h, а висоти дорівнюють
. Оскільки площа чергового прямокутника становить 
, то загальна площа гістограми дорівнює одиниці. По суті, гістограма — це графічний статистичний аналог щільності.Зобразимо гістограму абсолютних частот, задану таблицею 2.
Таблиця 2
| Частковий інтервал | 2-5 | 5-8 | 8-11 | 11-14 |
| Абсолютна частота | 9 | 10 | 25 | 6 |
П
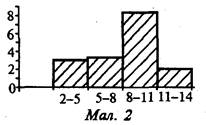отрібно визнати, що побудова полігонів і гістограм потребує певних зусиль обчислювального та графічного характеру (мал. 2). Тому для оперативного аналізу статистичних даних слугують такі їх спрощені характеристики, як. медіана і мода. Подамо їх означення.Медіаною випадкової вибірки називають той її елемент, який поділяє варіаційний ряд навпіл. У цьому означенні є певна неясність: якщо число елементів у вибірці парне, то середнього елемента не існує. В цьому випадку за медіану беруть два елементи, які знаходяться посередині вибірки. Тобто в таких випадках існують дві медіани, правда, вони можуть збігатися.
Модою випадкової вибірки називають значення того елемента, який трапляється найчастіше. Можна сказати, що поняття моди в даному контексті збігається, взагалі кажучи, з побутовим значенням цього слова. Наприклад, в певному магазині продають три типи шкільних ранців: на 3 кг ваги вмісту, на 4 і на 5 кг. Випадкова вибірка з 10 елементів виявилася такою: 5, 4, 5, 4, 5, 5, 3, 3, 5, 5. Складемо частотну таблицю (табл. 3).
Таблиця 3
| 3 | 4 | 5 |
| 2 | 2 | 6 |
Легко бачити, що варіанта 5 зустрічається найчастіше — 6 разів. Це і є мода даної вибірки.
35.Статистичні оцінки параметрів розподілу
Статистичною оцінкою невідомого параметра теоретичного розподілу називають функцію від випадкових досліджуваних величин, яка дає наближене значення оцінюваного параметра.Оцінки повинні бути незміщеними, ефективними та конзистентними (слушними, обґрунтованими).Незміщеною називають статистичну оцінку q*, математичне сподівання якої дорівнює оцінюваному параметру q, при будь-якому обсязі вибірки, тобтоМ(q*)=q.Зміщеною називають оцінку, математичне сподівання якої не дорівнює оцінюваному параметру.Ефективною називають статистичну оцінку, яка при даному обсязі вибірки має найменшу дисперсію.Слушною називають статистичну оцінку, яка прямує за ймовірністю оцінюваного параметра, коли n ® ¥ , тобто
.2.1. Генеральне та вибіркове середнєГенеральним середнім називають середнє арифметичне значень властивості генеральної сукупності.Якщо всі значення різні, то
,де N – обсяг генеральної сукупності.
Якщо значення властивості х1, х2 … хk мають частоти N1, N2 … Nk, то
.Вибірковим середнім називають середнє арифметичне значень властивості вибіркової сукупності.Якщо всі значення х1 … хn різні, то тут n – обсяг вибірки.
Якщо х1 має частоту n1, x2 – частоту n2, … xk – частоту nk відповідно, тоГруповим середнім називають середнє арифметичне значень властивості, які належать групі.
Загальним середнім називають середнє арифметичне значень властивості, що належать усій сукупності.
Загальне середнє дорівнює середньому арифметичному групових середніх, зважених за обсягами груп, а саме:де Nj – обсяг j-ї групи,
– групове середнє j-ї групи, N – обсяг вибірки.Вибіркове середнє є незміщеною оцінкою генерального середнього. Крім того, воно є також слушною оцінкою. Чим більший обсяг вибірки, тим менше вибіркове середнє відрізняється від генерального середнього.
36.Відхилення від загальної середньої, його властивості. Оцінка генеральної дисперсії по виправленій вибірковій
Середні величини характеризують значення ознаки, біля якої концентруються спостереження або, як ще кажуть, центральну тенденцію розподілу.
Середньою арифметичною статистичного ряду називають суму добутків усіх варіант на відповідні частоти, поділену на суму частот.
(1.1)
де xi – варіанти дискретного ряду (середини інтервалів інтервального статистичного ряду): ni – відповідні їм частоти. Можна бачити також, що
Властивості середньої арифметичної :
Середня арифметична постійної дорівнює власне постійній.
Якщо варіанти збільшити (зменшити) у одне і те саме число разів, то середня арифметична збільшиться (зменшиться) у стільки ж разів.
Якщо варіанти збільшити (зменшити) на одне і те саме число, то середня арифметична збільшиться (зменшиться) на те саме число.
Середня арифметична відхилень варіант від середньої арифметичньої дорівнює нулю.
Середня арифметична алгебраїчної суми декількох ознак дорівнює сумі середніх арифметичних цих ознак:
Якщо ряд складається з декількох груп, загальна середня дорівнює середній арифметичній групових середніх, при цьому вагами є об’єми цих груп.
При розв’язуванні задач можуть застосовуватися й інші форми середньої, які можна отримати із середньої ступеневої k-го порядку.
При k=1 отримаємо середню арифметичну, при k=-1 – середню гармонічну
При k = 0 (після розкриття невизначеності) – середню геометричну
При k=2 середню квадратичну.
Окрім розглянутих раніше середніх величин (їх називають аналітичними), в статистичному аналізі застосовують структурні або порядкові середні.
Медіаною Ме статистичного ряду називають значення ознаки, що припадає на середину ранжованого ряду спостережень.
Модою Мо статистичного ряду називають значення ознаки, якій відповідає найбільша частота.
Означення: Статистичною оцінкою невідомого параметру теоретичного розподілу називається функція від величин, що спостерігаються.
Для того, щоб статистична оцінка давала гарне наближення параметрів, що оцінюються, вони повинні задовольняти певним вимогам, до яких відносяться: незміщеність, ефективність та спроможність.
Означення: Незміщеною називається статистична оцінка
, математичне сподівання якої при довільному обсязі вибірки дорівнює параметру , що оцінюється, тобто 
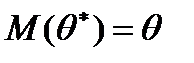. Зміщеною називається оцінка, математичне сподівання якої не дорівнює параметру, що оцінюється.Означення: Ефективною називається статистична оцінка, яка при заданому обсязі вибірки має найменшу можливу дисперсію.
При розгляді вибірок великого обсягу до статистичних оцінок застосовують вимогу спроможності.
Означення: Спроможною називається статистична оцінка, яка при
прямує за ймовірністю до параметру, що оцінюється.Наприклад, якщо дисперсія незміщеної оцінки при
прямує до нуля, то така оцінка є спроможною.Можна довести, що вибіркова середня є незміщена оцінка генеральної середньої, тобто
.Якщо за оцінку генеральної дисперсії прийняти вибіркову дисперсію, то ця оцінка буде приводити до систематичних помилок, надаючи занижене значення генеральної дисперсії. Пояснюється це тим, що вибіркова дисперсія є зміщеною оцінкою генеральної дисперсії, іншими словами, математичне сподівання вибіркової дисперсії не дорівнює генеральній дисперсії, що оцінюється. Тому для оцінки генеральної дисперсії за вибірковою дисперсією застосовують поправку Бесселя
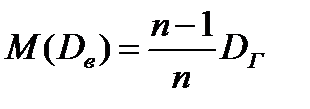
Легко виправити вибіркову дисперсію використовуючи поправку Бесселя, тоді виправлену дисперсію будемо позначати через
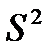
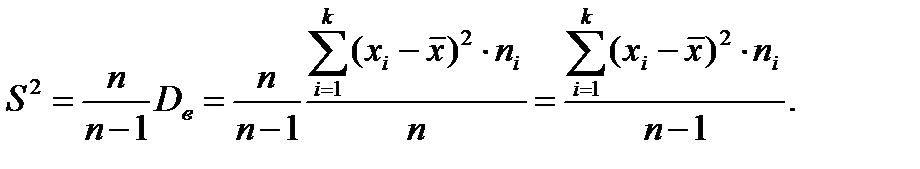
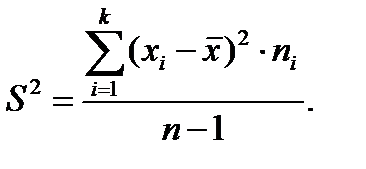
Як видно з формул виправленої
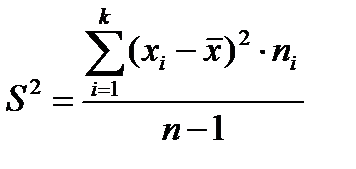і вибіркової 
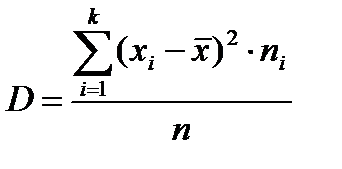дисперсій, вони відрізняються тільки знаменниками. Очевидно, що при досить великих обсягах вибірки вибіркова і виправлена дисперсії відрізняються мало. На практиці користуються виправленою дисперсією, якщо приблизно 
Виправлене середнє квадратичне відхилення визначається за формулою
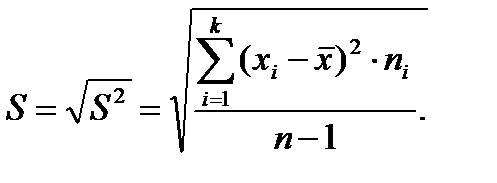
37.Точність оцінки, довірчі інтервали
Раніше нами була розглянута оцінка параметрів θ генеральної сукупності одним числом. Такі оцінки носять назву точкових. Однак точкова оцінка є лише наближеним значенням невідомого параметра θ навіть якщо вона незсунена, обґрунтована та ефективна, проте для вибірки малого об’єму може сильно відрізнятися від невідомого параметру θ.
Щоб мати більш точну та надійну оцінку параметра θ використовують, так звану, інтервальну оцінку.
Інтервальною оцінкою параметру θ називають числовий інтервал , який з заданою ймовірністю γ накриває невідоме значення параметру θ.
Звернемо увагу на те, що межі інтервалу знаходяться за вибірковими даними та є випадковими величинами. Інтервал називають довірчим, а ймовірність γ – довірчою імовірністю або надійністю оцінки. Поняття довірчого інтервалу ввели у 1950 р. Нейман та Пірсон. Також не важко побачити, що величина вибіркового інтервалу залежить від об’єму вибірки (зменшується із зростанням n) та від значення довірчої ймовірності γ (збільшується при наближенні її до 1).
У першу чергу розглянемо побудову довірчого інтервалу для генеральних середньої та частості w при достатньо великих вибірках (при n>30-40). Цей підхід побудовано на знані точного чи асимптотичного розподілу вибіркових характеристик.
У такому випадку довірчий інтервал обирається симетричним відносно параметру θ, тобто (θ-Δ, θ+Δ), а найбільше відхилення Δ вибіркової середньої (частості), від генеральної середньої (частості), яке можна задати з довірчою ймовірністю γ, називається граничною похибкою вибірки. За достатньо великою кількістю елементів вибірки користуючись центральною граничною теоремою можна довести наступне твердження:
Ймовірність того, що відхилення вибіркової середньої (або частості) від генеральної середньої (або частості), не перевищить Δ>0 дорівнює:
(1.6.1)
(1.6.2)
- функція (інтеграл ймовірностей Лапласа).
Формули (1.6.1), (1.6.2) отримали назву формул довірчої ймовірності для середньої та для частості.
38.Методи розрахунку зведених характеристик вибірки.
1 2 3 4 5 6 7